Sakana~
0%

【专题】动态规划1 线性/背包/区间dp

发表于 分类于

主要是记录牛客专题的dp基础题（都是一些比较典的题目）

由于我dp很烂，所以先从最简单的开始

【专题】动态规划1 线性/背包/区间dp

专题列表：https://ac.nowcoder.com/acm/contest/24213

（题目顺序随机，题目不全来自上述链接）

（呃呃Latex显示还是有问题，懒得搞图片了，反正点链接也可以看）

P2331 [SCOI 2005]最大子矩阵

https://www.luogu.com.cn/problem/P2331

题目描述

这里有一个n*m的矩阵，请你选出其中k个子矩阵，使得这个k个子矩阵分值之和最大。注意：选出的k个子矩阵不能相互重叠。

输入格式

第一行为n,m,k（1≤n≤100,1≤m≤2,1≤k≤10），接下来n行描述矩阵每行中的每个元素的分值(每个元素的分值的绝对值不超过32767)。

输出格式

只有一行为k个子矩阵分值之和最大为多少。

样例输入 #1

1
2
3
4
3 2 2
1 -3
2 3
-2 3

样例输出 #1

1
9

分析

由于只有两列，因此可以分两种情况拆开考虑。

m = 1 时，相当于求 k个最大连续字段，定义 f1[i][j] 表示 前i个数中取j段，转移则为：

  • 不取：f1[i][k] = max (f1[i][k], f1[i-1][k]);
  • 取：枚举上一个点 j，1[i][k] = max (f1[i][k], f1[j][k-1] + a[i] - a[j]);

m = 2 时，相当于上述问题的拓展，则给 dp 数组多加一维，定义 f2[i][j][k] 表示 左列前i个数,右列前j个数中取k个矩形，转移则为：

  • 左右都不取：f2[i][j][k] = max (f2[i-1][j][k], f2[i][j-1][k]);
  • 取左列：f2[i][j][k] = max (f2[i][j][k], f2[l][j][k-1] + s1[i] - s1[l]);
  • 取右列：f2[i][j][k] = max (f2[i][j][k], f2[i][l][k-1] + s2[j] - s2[l]);
  • 左右都取（前提是 i == j）：f2[i][j][k] = max (f2[i][j][k], f2[l][l][k-1] + s1[i] - s1[l] + s2[i] - s2[l]);

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <bits/stdc++.h>

using namespace std;
const int N = 105, M = 15;
int a[N], s1[N], s2[N], n, m, K;
int f1[N][M], f2[N][N][M]; 
//f1:前i个数中取k个矩形; f2:左列前i个数,右列前j个数中取k个矩形

int main () {
    cin >> n >> m >> K;

    //k个最大连续字段
    if (m == 1) {
        for (int i = 1; i <= n; i++)    cin >> a[i], a[i] += a[i-1];
        for (int k = 1; k <= K; k++) {
            for (int i = 1; i <= n; i++) {
                f1[i][k] = max (f1[i][k], f1[i-1][k]); //不取
                for (int j = 0; j < i; j++)     //取
                    f1[i][k] = max (f1[i][k], f1[j][k-1] + a[i] - a[j]);
            }
        }
        cout << f1[n][K];
        return 0;
    }

    //m = 2
    for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= 2; j++) {
            int x;  cin >> x;
            if (j == 1)     s1[i] = s1[i-1] + x;
            else            s2[i] = s2[i-1] + x;
        }  

    for (int k = 1; k <= K; k++) {
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                f2[i][j][k] = max (f2[i-1][j][k], f2[i][j-1][k]); //左右都不取
                for (int l = 0; l < i; l++)    f2[i][j][k] = max (f2[i][j][k], f2[l][j][k-1] + s1[i] - s1[l]); //取左
                for (int l = 0; l < j; l++)    f2[i][j][k] = max (f2[i][j][k], f2[i][l][k-1] + s2[j] - s2[l]); //取右
                if (i == j) {
                    for (int l = 0; l < i; l++) {
                        f2[i][j][k] = max (f2[i][j][k], f2[l][l][k-1] + s1[i] - s1[l] + s2[i] - s2[l]);
                    }
                }  //左右都取  
            }
        }
    }

    cout << f2[n][n][K];
    
}

//枚举行,把第i行到第j行压成一行 -> 单行求最大字串和

P1020 [NOIP1999 普及组] 导弹拦截

https://www.luogu.com.cn/problem/P1020

题目描述

某国为了防御敌国的导弹袭击，发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。某天，雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。

输入导弹依次飞来的高度，计算这套系统最多能拦截多少导弹，如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

输入格式

一行，若干个整数，中间由空格隔开。

输出格式

两行，每行一个整数，第一个数字表示这套系统最多能拦截多少导弹，第二个数字表示如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

样例输入 #1

1
389 207 155 300 299 170 158 65

样例输出 #1

1
2
6
2

提示

对于前 $50%$ 数据（NOIP 原题数据），满足导弹的个数不超过 $2000$ 个。该部分数据总分共 $100$ 分。可使用$\mathcal O(n^2)$ 做法通过。
对于后 $50%$ 的数据，满足导弹的个数不超过 $10^5$ 个。该部分数据总分也为 $100$ 分。请使用 $\mathcal O(n\log n)$ 做法通过。

对于全部数据，满足导弹的高度为正整数，且不超过 $5\times 10^4$。

此外本题开启 spj，每点两问，按问给分。

$\text{upd 2022.8.24}$：新增加一组 Hack 数据。

分析

重要性质：完整覆盖一个序列的不上升子序列的个数等于这个序列的最长上升子序列的长度

可以用反证法大致证明，（严格证明请参考偏序集的Dilworth定理）。

所以问题转化为 求最长下降子序列的长度 和 求最长上升子序列的长度。

直接暴力查找过不了，因为查找的区段内是有序的，所以可以使用二分。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <bits/stdc++.h>

using namespace std;
const int N = 1e5 + 5;
int a[N], f[N];

int main () {
    int n = 0, x;
    while (cin >> x) {
        a[++n] = x;
    }

    //最长下降子序列
    f[1] = a[1];
    int cur = 1;
    for (int i = 2; i <= n; i ++) {
        if (a[i] <= f[cur])     f[++ cur] = a[i];
        else {
            int pos = upper_bound (f + 1, f + cur + 1, a[i], greater<int>()) - (f); //找到第一个小于的前一个
            f[pos] = a[i];
        }
    }
    cout << cur << endl;

    //最长上升子序列
    f[1] = a[1];
    cur = 1;
    for (int i = 2; i <= n; i ++) {
        if (a[i] > f[cur])     f[++ cur] = a[i];
        else {
            int pos = lower_bound (f + 1, f + cur + 1, a[i]) - (f); 
            f[pos] = a[i];
        }
    }
    cout << cur << endl;

}

//重要性质:
//完整覆盖一个序列的不上升子序列的个数等于
//这个序列的最长上升子序列的长度

//问题转化为:
//1. 求最长下降子序列的长度
//2. 求最长上升子序列的长度

//优化:二分查找

P1091 [NOIP2004 提高组] 合唱队形

https://www.luogu.com.cn/problem/P1091

题目描述

$n$ 位同学站成一排，音乐老师要请其中的 $n-k$ 位同学出列，使得剩下的 $k$ 位同学排成合唱队形。

合唱队形是指这样的一种队形：设 $k$ 位同学从左到右依次编号为 $1,2,$ … $,k$，他们的身高分别为 $t_1,t_2,$ … $,t_k$，则他们的身高满足 $t_1< \cdots t_{i+1}>$ … $>t_k(1\le i\le k)$。

你的任务是，已知所有 $n$ 位同学的身高，计算最少需要几位同学出列，可以使得剩下的同学排成合唱队形。

输入格式

共二行。

第一行是一个整数 $n$（$2\le n\le100$），表示同学的总数。

第二行有 $n$ 个整数，用空格分隔，第 $i$ 个整数 $t_i$（$130\le t_i\le230$）是第 $i$ 位同学的身高（厘米）。

输出格式

一个整数，最少需要几位同学出列。

样例输入 #1

1
2
8
186 186 150 200 160 130 197 220

样例输出 #1

1
4

提示

对于 $50%$ 的数据，保证有 $n \le 20$。

对于全部的数据，保证有 $n \le 100$。

分析

观察合唱队列，可以发现他是一个，先上升后下降的队形，所以可以左边求一次上升序列，右边求一次下降序列，然后找出最长的这个序列，则得最小的出队人数

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <bits/stdc++.h>
#define int long long

using namespace std;
const int N = 105;
int n, a[N], l[N], r[N];

signed main () {
    cin >> n;
    for (int i = 1; i <= n; i++)    cin >> a[i];
    
    for (int i = 1; i <= n; i++) {
        l[i] = 1;
        for (int j = 1; j < i; j ++) {
            if (a[j] < a[i])    l[i] = max (l[j] + 1, l[i]);
        }
    }

    for (int i = n; i >= 1; i--) {
        r[i] = 1;
        for (int j = n; j > i; j --) {
            if (a[j] < a[i])    r[i] = max (r[j] + 1, r[i]);
        }
    }

    int ans = 0;
    for (int i = 1; i <= n; i++)    ans = max (ans, l[i] + r[i] - 1);
    cout << n - ans << endl;
}

//左边求一次上升序列，右边求一次下降序列

P 1282 多米诺骨牌

https://www.luogu.com.cn/problem/P1282

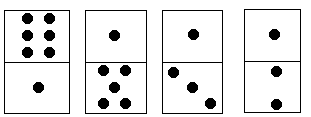
题目描述

多米诺骨牌由上下 $2$ 个方块组成，每个方块中有 $1\sim6$ 个点。现有排成行的上方块中点数之和记为 $S_1$，下方块中点数之和记为 $S_2$，它们的差为 $\left|S_1-S_2\right|$。如图，$S1=6+1+1+1=9$，$S2=1+5+3+2=11$，$\left|S_1-S_2\right|=2$。每个多米诺骨牌可以旋转 $180°$，使得上下两个方块互换位置。请你计算最少旋转多少次才能使多米诺骨牌上下 $2$ 行点数之差达到最小。

对于图中的例子，只要将最后一个多米诺骨牌旋转 $180°$，即可使上下 $2$ 行点数之差为 $0$。

输入格式

输入文件的第一行是一个正整数 $n(1\leq n\leq 1000)$，表示多米诺骨牌数。接下来的 $n$ 行表示 $n$ 个多米诺骨牌的点数。每行有两个用空格隔开的正整数，表示多米诺骨牌上下方块中的点数 $a$ 和 $b$，且 $1\leq a,b\leq 6$。

输出格式

输出文件仅一行，包含一个整数。表示求得的最小旋转次数。

样例输入 #1

1
2
3
4
5
4
6 1
1 5
1 3
1 2

样例输出 #1

1
1

分析

易得朴素的 dp：f[i][j]:前i个牌,上下差值为j，转移方程为：

f[i][j] = min (f[i-1][j-(a[i]-b[i])], f[i-1][j-(b[i]-a[i])]+1);

但是差值可能为负数，所以偏移一下。

*最大差值为(6-1)1000=5000,所以偏移5000

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <bits/stdc++.h>

using namespace std;
const int N = 1005, M = 5000*2 + 5, base = 5000; 
int n, f[N][M], a[N], b[N];

int main () {
    cin >> n;
    memset (f, 0x3f, sizeof f);
    f[0][base] = 0;
    for (int i = 1; i <= n; i++) {
        cin >> a[i] >> b[i];
        for (int j = -base; j <= base; j++) { //注意此处是[-base,base]
            f[i][j+base] = min (f[i-1][j-(a[i]-b[i])+base], f[i-1][j-(b[i]-a[i])+base] + 1);
        }
    }

    int l, r;
    for (int i = 0; i <= base; i++) {
        l = base + i, r = base - i;
        if ((f[n][l] != 0x3f3f3f3f) || (f[n][r] != 0x3f3f3f3f)) {
            break;
        }
    }

    cout << min (f[n][l], f[n][r]) << endl;
}


//f[i][j]:前i个牌,上下差值为j
//f[i][j] = min (f[i-1][j-(a[i]-b[i])], f[i-1][j-(b[i]-a[i])]+1);
//最大差值为(6-1)*1000=5000,所以偏移5000
//5000代表0

Bitset 优化背包

https://ac.nowcoder.com/acm/contest/24213/1035

题目

分析

朴素转移：f[i][j] |= f[i-1][j-x[i]*x[i]] = 1;

对于这种一行可以表示为一个01串，且变化都是整体偏移的，可以使用 bitset 优化空间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <bits/stdc++.h>

using namespace std;
const int N = 1e6 + 5;
bitset<N>f[105];

int main () {
    int n;
    cin >> n;
    f[0][0]= 1;
    for (int i = 1; i <= n; i++) {
        int l, r;
        cin >> l >> r;
        for (int j = l; j <= r; j++) {
            f[i] |= f[i-1] << (j * j);
        }
    }
    cout << f[n].count();
}

//bitset优化,左移k^2

P1052 [NOIP2005 提高组] 过河

https://www.luogu.com.cn/problem/P1052

题目描述

在河上有一座独木桥，一只青蛙想沿着独木桥从河的一侧跳到另一侧。在桥上有一些石子，青蛙很讨厌踩在这些石子上。由于桥的长度和青蛙一次跳过的距离都是正整数，我们可以把独木桥上青蛙可能到达的点看成数轴上的一串整点：$0,1,\cdots,L$（其中 $L$ 是桥的长度）。坐标为 $0$ 的点表示桥的起点，坐标为 $L$ 的点表示桥的终点。青蛙从桥的起点开始，不停的向终点方向跳跃。一次跳跃的距离是 $S$ 到 $T$ 之间的任意正整数（包括 $S,T$）。当青蛙跳到或跳过坐标为 $L$ 的点时，就算青蛙已经跳出了独木桥。

题目给出独木桥的长度 $L$，青蛙跳跃的距离范围 $S,T$，桥上石子的位置。你的任务是确定青蛙要想过河，最少需要踩到的石子数。

输入格式

输入共三行，

  • 第一行有 $1$ 个正整数 $L$，表示独木桥的长度。
  • 第二行有 $3$ 个正整数 $S,T,M$，分别表示青蛙一次跳跃的最小距离，最大距离及桥上石子的个数。
  • 第三行有 $M$ 个不同的正整数分别表示这 $M$ 个石子在数轴上的位置（数据保证桥的起点和终点处没有石子）。所有相邻的整数之间用一个空格隔开。

输出格式

一个整数，表示青蛙过河最少需要踩到的石子数。

样例输入 #1

1
2
3
10
2 3 5
2 3 5 6 7

样例输出 #1

1
2

提示

【数据范围】

  • 对于 $30%$ 的数据，$1\le L \le 10^4$；
  • 对于 $100%$ 的数据，$1\le L \le 10^9$，$1\le S\le T\le10$，$1\le M\le100$。

【题目来源】

NOIP 2005 提高组第二题

分析

石子很少,可以离散化

石子距离 >s*t 就直接离散化（但是具体为啥不是很清楚。。。）

（良心题解：https://www.luogu.com.cn/blog/Actinoi/solution-p1052）

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <bits/stdc++.h>

using namespace std;
const int N = 105, M = 10005, K = 1e5 + 5;
int a[N], sum[M];
bool st[K];  //离散化后的石头位置
int l, s, t, m;

int main () {
    cin >> l >> s >> t >> m;
    memset (sum, 0x3f, sizeof sum);
    for (int i = 1; i <= m; i++)  cin >> a[i];
    sort (a + 1, a + m + 2);

    int x = 0;
    for (int i = 1; i <= m + 1; i++) {
        int dx = a[i] - a[i-1];
        if (dx <= t * s)     x += dx;
        else    x += dx % t  + t; //离散化
        st[x] = true;
    }

    sum[0] = 0;
    for (int i = 1; i <= x + t; i++) { //跳出去也算
        for (int j = s; j <= t; j++) {
            if ((i - j) >= 0)   sum[i] = min (sum[i], sum[i-j] + st[i]);
        }
    }

    int ans = 1e9;
    for (int i = x; i <= x + t; i++)    ans = min (ans, sum[i]);
    cout << ans;
}

//石子很少,可以离散化
//石子距离 >s*t 就直接离散化

C. Mr. Kitayuta, the Treasure Hunter

https://codeforces.com/contest/505/problem/C

分析

朴素 dp ：f[i][j]:在i,到i时跳了j，转移：f[i][j] = max (f[i-j][j-1], f[i-j][j+1])+a[i];

和多米诺骨牌那题很像，注意因为每次跳的距离是基于 d 开始变化的，所以只需记录与其差值即可。

(1+2+...+n)<=30000 -> n < 300，估算一下发现要偏移 300。

记得初始化

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <bits/stdc++.h>

using namespace std;
const int N = 30005, M = 605, base = 300;
int n, d, f[N][M], a[N], x;

int main () {
    cin >> n >> d;
    for (int i = 0; i < n; i++) {
        cin >> x;
        a[x] ++;
    }

    memset (f, -0x3f, sizeof f); //！！
    int ans = f[d][base] = a[d];
    for (int i = d + 1; i <= x; i++) {
        for (int j = -base; j <= base; j++) {
            int dx = d + j; //i-dx: 实际位置
            if (dx <= 0 || dx > i)  continue;
            f[i][j+base] = max (f[i-dx][j-1+base], f[i-dx][j+1+base]) + a[i];
            f[i][j+base] = max (f[i-dx][j+base] + a[i], f[i][j+base]);
            ans = max (f[i][j+base], ans);
        }
    }
    
    cout << ans;

}


//(1+2+...+n)<=30000  -> n < 300
//故差值不超过300,记录一下偏移
//记录与d的差值,然后偏移一下

//f[i][j]:在i,到i时跳了j
//f[i][j] = max (f[i-j][j-1], f[i-j][j+1])+a[i];

D. Fox And Jumping

https://codeforces.com/contest/510/problem/D

分析

取第i个数代价为 ci , 取出若干数使得其最大公约数为1的最小代价

朴素 dp：f[i][j]: 前i个数,gcd为j，转移：f[i][j]=min(f[i-1][j], f[i-1][k]+ci); //后者取到的条件是gcd(k,li)==1

优化：n小 l[i] 大 -> 很疏松 -> map存

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <bits/stdc++.h>

using namespace std;
const int N = 305;
int l[N], c[N], n;
map<int, int> mp;

int main () {
    cin >> n;
    for (int i = 1; i <= n; i++)    cin >> l[i];
    for (int i = 1; i <= n; i++)    cin >> c[i];

    mp[0] = 0;
    for (int i = 1; i <= n; i++) {
        auto tp = mp;
        for (auto pi : tp) {
            int x = __gcd(pi.first, l[i]), y = pi.second + c[i];
            if (!tp.count(x))    tp[x] = y;
            else    tp[x] = min (tp[x], y);
        }
        swap (tp, mp);
    }

    if (mp[1] == 0)     mp[1] = -1;
    cout << mp[1];
}


//取第i个数代价为ci,取出若干数使得其最大公约数为1的最小代价
//f[i][j]: 前i个数,gcd为j
//f[i][j]=min(f[i-1][j], f[i-1][k]+ci); //后者取到的条件是gcd(k,li)==1
//n小li大 -> 很疏松 -> map存

Brackets

http://poj.org/problem?id=2955

大意：求括号序列中匹配的括号数

分析

大体上可以分为两种匹配规则：相邻的直接匹配 或者 由外向内进行匹配，要在这两种策略下进行合理的抉择，使得总匹配数最大。

  • 直接相邻匹配：f[l][r] = max (f[l][r], f[l][k] + f[k+1][r]);
  • 由外向内拓展：区间 dp，f[l][r] = (len > 2 ? f[l+1][r-1] : 0) + 2;

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>
#include <cstring>
#include <cmath>

using namespace std;
const int N = 105;
int f[N][N]; //区间[i,j]
string s;

void solve () {
    memset (f, 0, sizeof f);
    int n = s.size();
    for (int len = 2; len <= n; len++) {
        for (int l = 0; len + l - 1 < n; l++) {
            int r = len + l - 1;
            if (s[l] == '(' && s[r] == ')' || s[l] == '[' && s[r] == ']')
                f[l][r] = (len > 2 ? f[l+1][r-1] : 0) + 2;
            for (int k = l; k < r; k++)
                f[l][r] = max (f[l][r], f[l][k] + f[k+1][r]);
        }
    }
    cout << f[0][n-1] << endl;
}

int main () {
    while (cin >> s, s != "end") {
        solve ();
    }
}

//两种匹配策略
//1. 大包小,区间dp
//2. 相邻匹配